Models can do calculus better than you
I'm sorry, I don't make the rules
Do you remember high school or early college calculus? Yeah — me neither. Thankfully, most language models (even the really good ones) aren’t able to master basic STEM tasks either. Here’s OpenAI’s text-davinci-002 attempting to answer it:
And here’s a bunch of other models being wrong, courtesy of nat.dev (check it out!):
Despite techniques like chain of thought and scratchpad, long-range step-wise reasoning is an area models severely struggle with. Interestingly, it seems like the fix to this is quite an intuitive approach.
Today, we’re discussing “Solving Quantitative Reasoning Problems with Language Models”, by Google Research.
Introduction and Motivation
Goal: Allow large language models to develop mathematical and scientific reasoning abilities.
Core Insight: Fine-tuning as a process allows models to specialize in a particular domain. Then, backed by understanding of topics through pre-training, models are substantially better at specific tasks than before.
Solution: Fine-tune the PaLM series of models on specificity research and college-level STEM course data. The hypothesis is that this would improve quantitative reasoning of the model.
Here’s what Minerva can do:
Development Details
This is what the fine-tuning dataset looks like:
The dataset is surprisingly small — only 35B tokens. In comparison to the 1T tokens or so needed to train the underlying PaLM model, this is a small quantity and therefore can be an extremely high-quality dataset.
They also were able to particularly collect problems with automatically verifiable solutions (like numbers or verification using symbolic execution) — proofs and short answers were therefore disqualified.
The last interesting detail is that the paper does not use the standard pass@k approach to model querying. pass@k means you attempt to generate an answer k times, and return True if any one of them return the correct answer. Instead, they use a maj1@k method, where they generate k answers, and take the majority answer. This is for a few reasons:
The pass@k model keeps improving as k grows larger, because they only check solutions. This means that the model can get false positives at larger k and improve its accuracy falsely.
The maj@k system is a good metric for a mathematical problem — there are many ways to be wrong, but only one or few ways to be right. Thus, the majority model coalesces the right answers more than it does the wrong ones.
Evaluation
Let me jump to the juicy bit — Minerva outperforms previous models on just about everything.
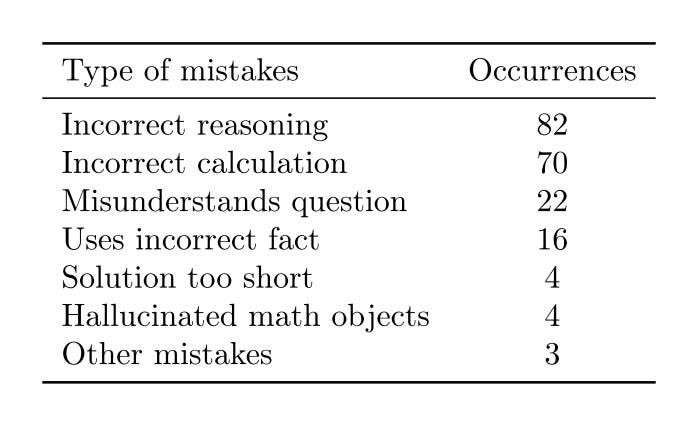
Yes, it is quite wild that such a simple fine-tuning technique is able to achieve this. An analysis of the types of mistakes Minerva makes is also very interesting:
Finally, the paper wonders if Minerva is weakly or strongly memorizing the solutions— either through data leakage or weak pattern matching. To check this, they 1) change the wording of the problem and 2) modify the numbers of the problem. Data below:
In both cases, the accuracies are correlated, with no clear bias in favor of the original formulation.
Limitations and Future Work
For sure a nitpick to start with: I don’t see how the data below is, as the paper argues, correlated. It does seem like the model is sensitive to modified numbers, if I’m reading this graph right.
I would be very interested in seeing future work attempt to incorporate proofs and short answer type questions as well. I would be interested in seeing if different types of STEM problems tends to improve learning in other styles of questions as well.
I also think that the model should be given access to external tools — you wouldn’t expect a human to remember what the square root of 7 is off the top of their head either. While I understand why they left it out of this paper for the sanctity of the research methodology, I would love to see future work experiment with this.
In Summary
This is one of those papers that makes me a little bit mad — because the idea is so dead simple, and the execution so cleanly done, that it makes me wonder why I hadn’t thought of and done this too. And Minerva’s ability are extremely impressive:
I think this paper really shows the value of fine-tuning a large pre-trained model with high-quality data — doing it well leads to extremely positive results.
I also think it’s a great exploration of how far we are from actually making “intelligence”. A great example — Minerva learned to do 8-digit addition (awesome) but fails at 12-digit addition (sad). If it had truly understood the concept of addition, no number of digits would trip it up anymore. How can future work add enough inductive biases such that we could reliably start teaching our models concepts?
Truly a question for the ages. Until next time!