Quadratic Complexity holds back the legendary transformer (Part 1)

The next generation of architectures.

You know what the transformer is. It is the neural architecture that lies under all the greatest large language models of today — PaLM, GPT-3, GPT-4, OPT, Llama, Alpaca, all of it.

You’ve also maybe heard of “context lengths”. This is the maximum window of text that a model can attend to. One of GPT-4’s great achievements is that it has a maximum of 32K tokens in context, equivalent to 52 pages of text. In comparison, previous token length was around 8K.

First, why does this context length exist? This is, surprisingly, not a model problem but a compute problem. The core of transformers — the attention mechanism — is quadratic in the length of the sequence. This restricts the sequence from growing too large. This is perhaps the biggest restrictions on neural model efficiency right now.

How are people making it better? Many ways! Ranging from I/O memory read-write optimizations, to approximations and more. We previously covered FlashAttention, which tackles this problem from the perspective of “kernelizing” operations to reduce data movement.

FlashAttention challenges ML researchers to think about systems-level improvements

Over the next week, we’ll take a grand tour of the recent burst of research in this domain. We’ll talk about approximations, replacements with kernels, and how systems can be used to improve AI design.

Today, we’re focusing on the first one — improving attention using approximation techniques. We’re reading “Memorizing Transformers”, by Google.

Introduction and Motivation

Goal: Increase the context-length of a transformer, such that it can attend to text with long-range strict dependencies like code, proofs, books, or webtext.

Core Insights:

1. Attention is just an approximated hash table. Instead of attending to an exact answer to a “query”, we attend to a weighted combination of our values, based on how similar the “key” and the “query” are.

2. The key, query and values are recomputed and adjusted to be more accurate through every back-propagation (training loop), which is why we can’t simply store them in memory.

3. If we accept some staleness in our key/value pairs, we can move those key values that are moving out of attention window into some external memory.

4. Once these are stored, we can access them and add this “external retrieval” step to our attention mechanism!

Development Details

The idea of storing key value pairs is fairly straightforward — we take the vectors, and put them in a database! The complications arise in the next two steps: How do we retrieve them, and how do we use them?

Retrieval is tricky because 1) we cannot send all of our external memory attention to the model — this would defeat the purpose of not having the model be quadratic. 2) we cannot find the k most similar values, because this would be too computationally expensive. For this reason, we use k nearest neighbors, to find the approximate top-k key, value pairs for a given query.

Using these retrieved vector is also tricky! How do you balance local attention and external memory attention? The paper’s solution — let the model learn how to balance them. Interpolate them with some value between (0, 1).

Sigmoid function creates (0, 1) value.

Evaluation

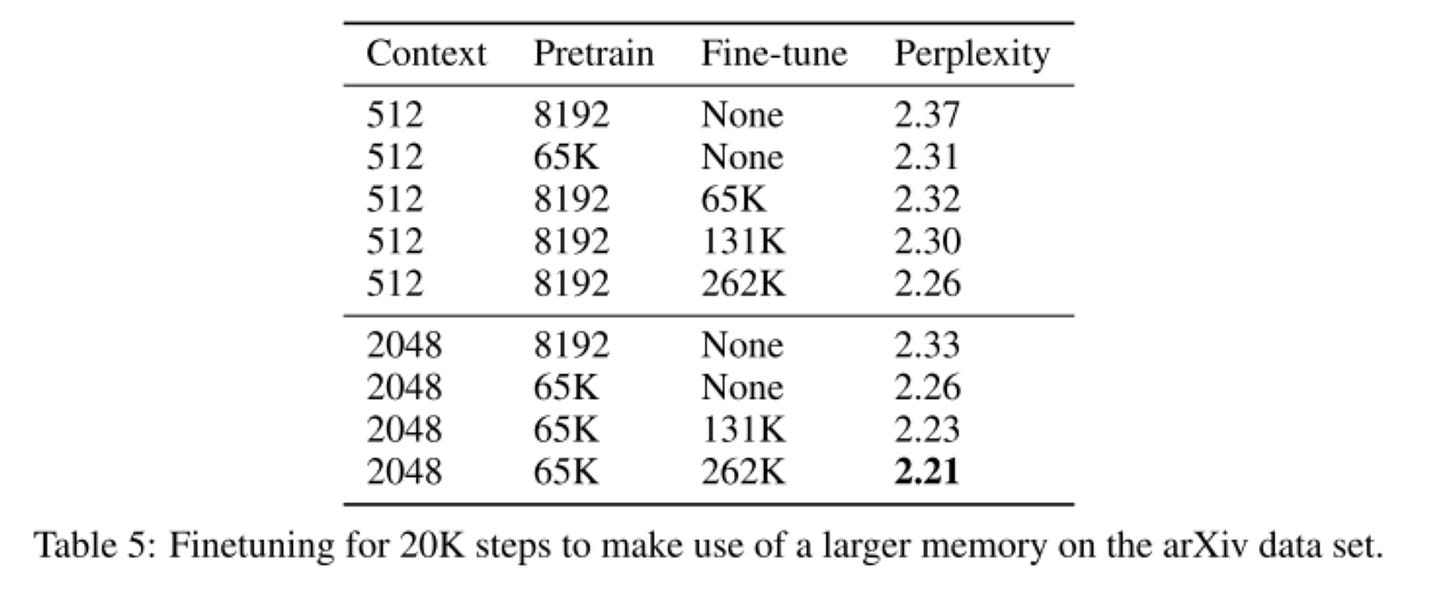
Here’s the big finding of the paper — the perplexity of the memorizing transformer is lower than the vanilla transformer at every size. Perplexity is, vaguely, a measure of how surprised the model is by a new set of words. Lower perplexity means a more well-learned models.

The longest context + the largest memory + the largest cache leads to the lowest perplexity value.

However, they also discovered that, at training, the model occasionally became unstable because of stale external memory. Thus, it was found to be better to train with a smaller memory and have a larger one at inference time.

Limitations and Future Work

1. I find the problem of model instability because of staleness quite interesting. Their solution — just keep the memory smaller — is not satisfactory for the long term, in my opinion. I would rather see techniques for the lower weighing of staler attention

2. A Memorizing Transformer does not need to be pre-trained from scratch; it is possible obtain large gains from adding memory to an existing pre-trained model, and then fine-tuning it. As such, I would have liked to see the memory mechanism applied on more off-the-shelf models.

3. I’d have liked to see an evaluation against specific models like Minerva (for math) or Codex (for code) to demonstrate the capabilities of the model against specific SOTAs.

In Summary

The current trend of scaling models to improve them has led to some fantastic and impressive research. However, I worry that architecture improvements to the model tend to get lost in the noise.

This paper is a pretty great marriage between systems-level ideas (of caches and external memory retrieval with kNN search) and the transformer architecture. Our current state-of-the-art models do not leverage the systems resources available to them efficiently. Who knows when someone might create “the next transformer”, but there is a lot of work to be done to make our current model optimal.

Until next time!