Winning the AI Lottery by Buying a Lot of Tickets
The Lottery Ticket Hypothesis, and why models are so big today
The founder of HuggingFace recently tweeted a fact that surprised me:


For large models, inference model size =/= training model size, most of the time. This is because training can take as long as you’d like, but inference needs to be real-time fast.
How are models made smaller? Many techniques exist — like pruning, quantization and distillation. I find these to be really interesting techniques, and will be covering them a lot more over the next few weeks (as I dive more into them myself!)
But today, let’s talk pruning. At a high level, pruning is removing the nodes and connections in a neural net that aren’t contributing to the model’s accuracy. This creates a sparse model, which are typically easier for GPUs to store and run operations on, thus making inference time faster and cheaper.
In 2019, MIT gave us the “Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks”. This was best paper at ICLR 2019, and remains to this day one of the most well-known AI papers out there.
So let’s jump right into it!
Introduction and Motivation
Goal: Most models these days are over-parameterized — you could prune them to be ~90% smaller without losing any of the accuracy. Wouldn’t it be wonderful if we could simply train smaller models to begin with?
Hypothesis: “A randomly-initialized, dense neural network contains a subnet-work that is initialized such that—when trained in isolation—it can match the test accuracy of the original network after training for at most the same number of iterations.”
That is to say, only a small number of connections and nodes matter in a very large neural network. If we were to be able to find this “winning ticket”, we wouldn’t need to train a large model at all!
Development Details
So, can we train a small model from the beginning? Short answer: No.
Roll credits. Until next time!
Just kidding — even if we can’t get to the pruned model in one go, we can use this hypothesis to find this model faster. The reason we can’t one-shot is that we need to know a great initialization for the network to reach this pruned state. This great initialization is only found, for now, by training a much larger network (“buying a whole lot of tickets”).
Instead, we suggest an iterative pruning technique that allows us to incrementally make the model smaller throughout training:
Randomly initialize your network with weights W
Train a full neural network for some j iterations
Prune p% of the parameters (here, those with the least magnitude), creating a mask m
Reset the remaining parameters to the initial weights W, now using the mask m to not set the pruned params
This technique identifies the connections not contributing to the output as much, prunes them. The core intuition here is that the responsibility for what those nodes did learn is now delegated to other nodes (similar to dropout’s behavior if you’re familiar).
Evaluation
If there’s one thing this paper does not skimp on, it’s data. Oodles and oodles of data. I’ll cover some of it here!
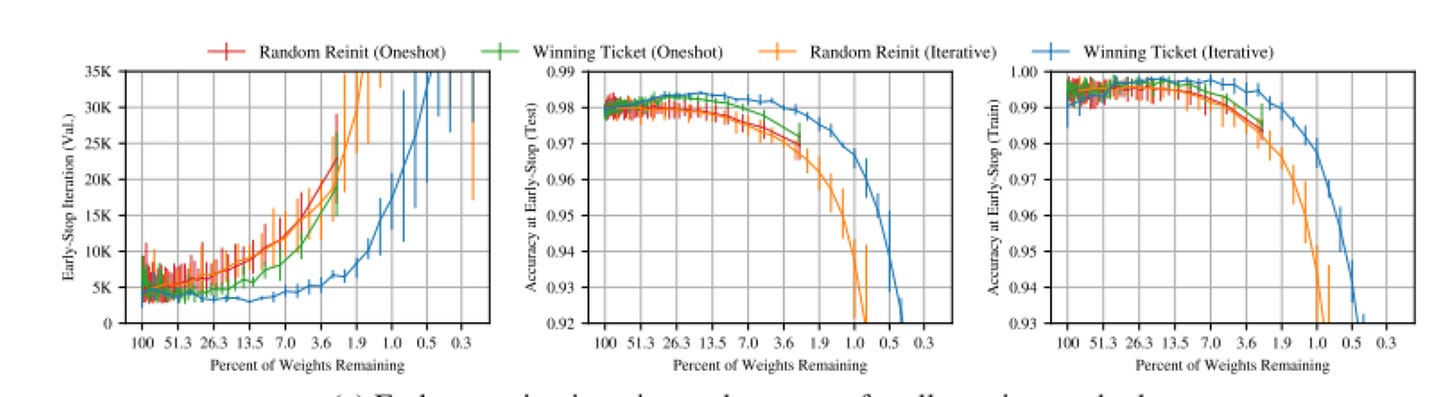
First, we evaluate the performance of pruning on LeNets. We see that the pruned models (green line) have higher test accuracy than the unpruned models (deep blue line).
Moreover, the model where weights are reinitialized (light blue line) are less accurate than models that keep their initial weights, suggesting that the initialization is part of the winning ticket as much as the model structure retained. They confirm this in an ablation study, which also demonstrates that the iterative techniques performs better than the one-shot approach of train-then-prune:
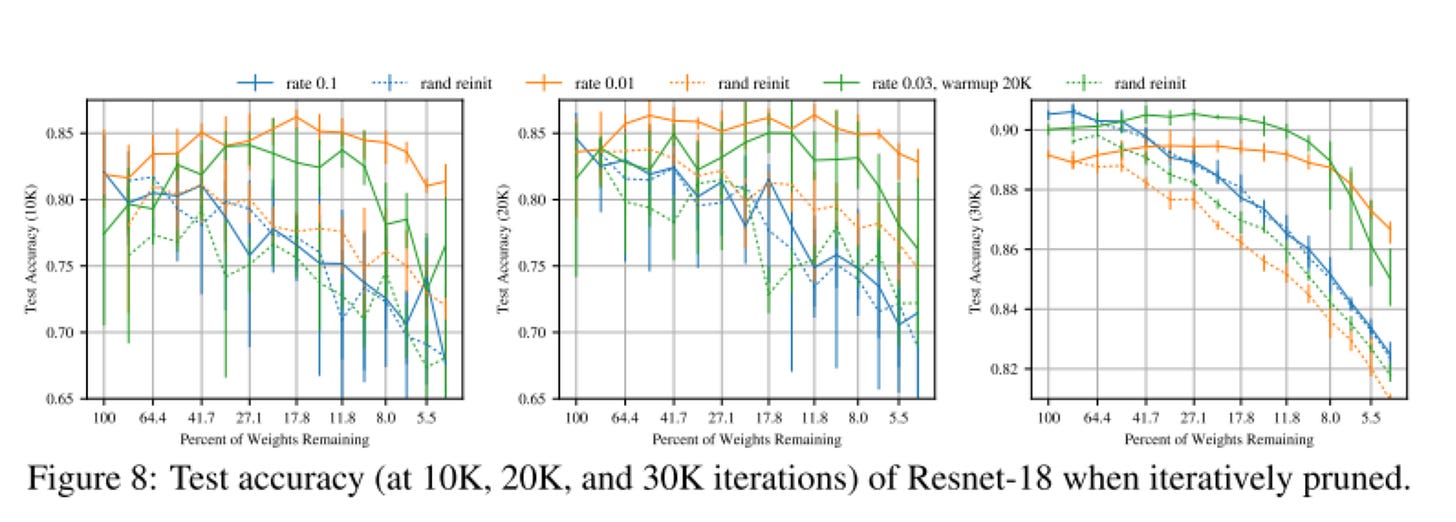
We see similar performance on large image models, though large models tend to be a lot more sensitive to learning rate during iterative pruning and require warmup in learning rate to be able to find the winning ticket.
The Lottery Ticket Hypothesis seems to exhibit an Occam’s Hill — models that are too big are too complex to generalize, models that are too small are not expressive enough. (Yes, Occam’s Hill is just a fancy CS term for a Goldilocks situation).
Limitations and Future Work
The paper tests its technique on mostly smaller models and datasets — this is because the lottery ticket technique is quite computationally expensive (multiple model iterations). Interesting future work could (and did!) address attempting to test the hypothesis on large scale models.
The paper is also tested solely on vision centric-tasks. I’m not sure it fits in the modern transformers paradigm, where the model architecture is much more complicated and it’s substantially harder to prune chunks out.
The paper shows that the initializations are a big part of the winning ticket. Future work should investigate the properties of these initializations such that, with the pruned network, they enable better learning.
On bigger networks, the paper utilized learning rate warmup to reach a lottery ticket. It would be interesting to explore why this warmup is necessary.
In Summary
In ML terms, this paper is quite old — it was written before GPT-3 was even in production. It’s been disproven, debunked, then re-proven — anyone interested should definitely look into the Lottery Ticket Saga. Mostly, I appreciate this paper’s attempt to explain some of the why behind ML models. This nature of work is lost in the frantic pace of improving models, but might be even more critical in the long run.
What’s the core insight? That sparsity is all-important in NNs. Sparse networks are better for storing, training, and compute — and there is a lot of exciting on-going work in this field. Most models today are over-parameterized — it is important to explore how to make them smaller.
Last, I’d encourage everyone to read the first author, Jonathan Frankle’s retrospective on this paper. It’s thoughtful and insightful and a great look into how to do great CS research.
Until next time!